CRITERIOS
DE DIVISIBILIDAD
Un elemento q de un anillo A es divisible por otro elemento
t si existe un p tal que :
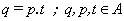
Decimos entonces que t divide a q y q se denomina múltiplo
del elemento t, siendo t divisor del elemento q.
En el anillo de los enteros existen reglas para determinar
si un elemento es divisible por otro. La validez de estas
reglas puede determinarse por diversos métodos
entre los que cabe citar el método de congruencias
o aritmética modular [1], [2].
En lo que sigue, expondremos un método general
para obtener criterios de divisibilidad para cualquier
elemento de un anillo asociativo conmutativo.
Para cualquier conjunto de n elementos de un anillo con
un divisor común, tenemos :
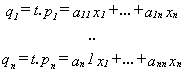
donde cada aij y cada xk son elementos del anillo considerado.
El sistema de ecuaciones expuesto puede agruparse en forma
matricial :
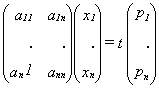
Y de esta ecuación, mediante los métodos
del álgebra lineal, podemos despejar cada xi en
función del resto de los elementos
Siendo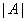 
el
determinante de la matriz {aij} dada en (3) y Ri la componente
i-ésima del producto de la matriz traspuesta de
la adjunta de {aij} y el vector P.
Todos los factores anteriores son elementos del anillo
A [1] con lo que podemos poner :
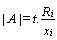
En este caso (Ri/xi) es necesariamente un elemento del
anillo A puesto que 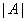y
t lo son. Todo lo anterior implica que 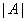es
múltiplo de t.
APLICACIONES AL ANILLO
DE LOS ENTEROS
1º. regla de divisibilidad por 9 (y 3) : 9 = 10-1
= 10.1 + 1.(-1)
Si escribimos cualquier número en la forma :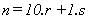 
tendremos :
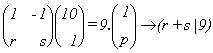
y a partir de ahí diremos que n es múltiplo
de 9 (de 3) si lo es la suma de sus componentes r y s.
Aplicando reiteradamente el resultado obtenido a un número
de la forma (10) :
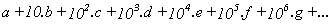
tendremos :
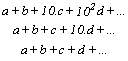
y llegamos a la regla ya conocida: "Un número
es divisible por 9 o por 3 cuando lo es la suma de sus
cifras".
2º.- Regla de divisibilidad por 11 : 11 = 10 + 1
= 10.1 + 1.1
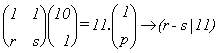
tomando para n la expresión dada en (10) obtenemos
:
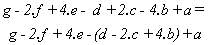
y aplicando la relación obtenida a la ecuación
(7), obtenemos la regla de divisibilidad por 11 : "Un
número es divisible por 11 cuando la diferencia
entre la suma de las cifras pares y las impares es múltiplo
de 11 o cero".
3º.- Regla de divisibilidad por 7
Tenemos : 7x3 = 21 = 20 + 1 = 2.10 + 1.1 ; 7x7 = 49 =
50 - 1 = 5.10 + 1.(-1)
y resultan las expresiones :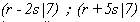 
que son formalmente iguales si consideramos que se cumple
: 
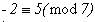
Tomando la primera de ellas y aplicándola iteradamente
a un número de la forma (7) resulta :
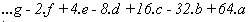
Pero teniendo en cuenta equivalencias modulares respecto
al número 7 podemos escribir :
y podemos enunciar la regla según la cual: "Un
número es divisible por 7 si una vez su cifra más
significativa menos 2 veces su siguiente cifra más
4 veces su siguiente cifra menos una vez ... es cero o
múltiplo de 7"
EJEMPLO 1
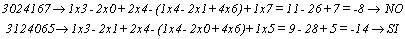
Cualquier otra regla que queramos deducir es equivalente
a la obtenida, sea cual sea el número de factores
que tomemos.
De modo análogo obtenemos las siguientes reglas
de divisibilidad :
para 13 
r + 4.s ; r - 9.s ; para 17
r - 5.s ; r + 12.s
para 19
r + 2.s ; r - 17.s ; para 23
r + 7.s ; r - 16.s
para 29
r + 3.s ; r - 26.s ; para 31
r - 3.s ; r + 28.s
para 37
r - 11.s ; r + 26.s ; para 41
r - 4.s ; r + 37.s
para 43
r + 13.s ; r - 30.s ; para 47
r - 14.s ; r + 33.s
para 53
r + 16.s ; r - 37.s ; para 59
r + 6.s ; r - 53.s
para 61
r - 6.s ; r + 55.s ; para 67
r - 20.s ; r + 47.s
para 71
r - 7.s ; r + 64.s ; para 73
r + 22.s ; r - 51.s
para 79
r + 8.s ; r - 71.s ; para 83
r + 25.s ; r - 58.s
para 89
r + 9.s ; r - 80.s ; para 97
r - 29.s ; r + 68.s
Escribiendo un número natural en la forma :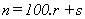 
podemos obtener, entre otras, las siguientes reglas de
divisibilidad:
para 11
r + s ; para 101
r - s
Escribiendo un número natural en la forma :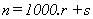 
podemos obtener, entre otras, las siguientes reglas de
divisibilidad:
para 37
r + s ; para 13
r - s ; para 7
r - s
CRITERIOS DE DIVISIBILIDAD
(APLICACIONES)
Proposición 1
.- Si se cumple :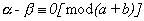 
,
entonces, la expresión :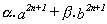
(14) es múltiplo de (a+b) para todo n natural
Demostración
Sea (a+b) = c. Para cualquier número natural t
podemos escribir: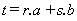 
donde
r y s son números naturales.
Teniendo en cuenta el algoritmo de obtención de
criterios de divisibilidad, si t es múltiplo de
c, se cumplirá que r-s también lo es. En
esas condiciones podemos escribir :
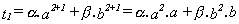
y, por tanto :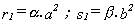 
,
con lo cual :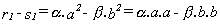 
y, a partir de ahí :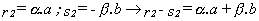 
Pero teniendo en cuenta la hipótesis de partida,
resulta :
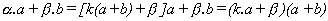
lo que significa que , para n = 1, la expresión
considerada es múltiplo de c = (a+b).
Supongamos ahora que la expresión (14) es múltiplo
de c para un valor dado de n; entonces :
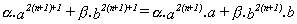
Y así :
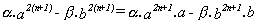
por lo que :
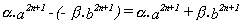
y, por la hipótesis de inducción, queda
demostrado lo que nos proponíamos.
Corolario
La expresión :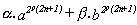 
es múltiplo de 
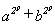cuando
se verifica que :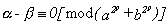 
EJEMPLO 2.-
Para la expresión :[2]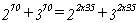 
se cumple lo dicho, por lo que podemos decir que es múltiplo
de 13
Proposición 2
Si se cumple :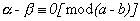 
entonces, la expresión : 
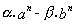(27)
es múltiplo de (a-b) para todo n natural
Demostración
Teniendo en cuenta el algoritmo de obtención de
criterios de divisibilidad, cualquier número de
la forma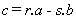 
será múltiplo de (a-b) si lo es (r+s).
Para n = 1 y teniendo en cuenta la hipótesis de
partida, podemos escribir :
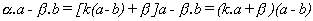
Sea ahora n un número par. Para la expresión
(27) tenemos :
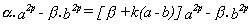
y desarrollando :
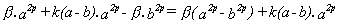
Pero se cumple :
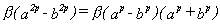
por lo que, para n par, la expresión (27) será
múltiplo de (a-b) si lo es para n impar.
Sea entonces n = 2p+1 y supongamos que :
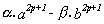
es múltiplo de (a-b). Tenemos :
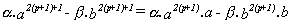
La anterior expresión será múltiplo
de (a-b) si lo es
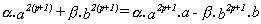
que, a su vez, lo será si lo es :
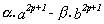
pero, por la hipótesis de inducción, sabemos
que ello es cierto, por lo que queda demostrado lo que
nos proponíamos.
EJEMPLO 3.-
La expresión [2] :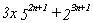 
es múltiplo de 17 para todo n natural, ya que se
tiene :
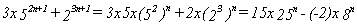
y como se cumple : 15 - (-2) = 17 ; 25 - 8 = 17, resulta
lo dicho.
EJEMPLO 4.-
La expresión [2] :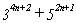 
es múltiplo de 14 para todo n natural, ya que se
tiene :
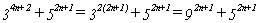
y puesto que 9+5 = 14, tenemos lo dicho.
EJEMPLO 5.-
La expresión [2] :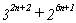 
es múltiplo de 11 para todo n natural, ya que se
tiene :
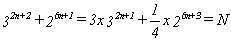
y quitando el denominador :
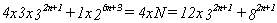
con lo que resulta :
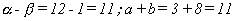
y hemos demostrado lo que queríamos.
EJEMPLO 6.-
La expresión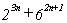 
es
múltiplo de 7 para todo n natural, ya que se tiene
:
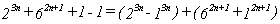
y cada uno de los sumandos obtenidos es múltiplo
de 7.
EJEMPLO 7.-
Para demostrar que se cumple : (37)
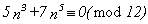
para todo n entero [3], podemos considerar un número
de la forma :
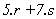
con lo que tendremos : 12 = 5 + 7 = 5.1 + 7.1
Y, por tanto, (37) será múltiplo de 12 si
lo es (r-s). Tenemos (38)
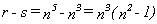
y (37) se verificará si (38) es múltiplo
de 12.
Si n es par, tenemos :
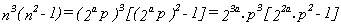
Está claro que el término fuera del corchete
es múltiplo de 4 para cualquier valor de a y p
(siendo p primo).
El término de dentro del corchete se puede poner
: 
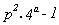y su valor será múltiplo de 3 si lo es :
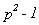; pero ello es cierto según el teorema de Euler-Fermat.
Si n es impar, entonces el término entre paréntesis
de (38) es múltiplo de 12 ya que, por una parte,
es múltiplo de 3 según sabemos por el teorema
de Euler-Fermat y, por otra, se puede poner en la forma
:
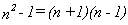
y cada uno de los factores resultantes es par.
EJEMPLO 8.-
La expresión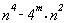 
es
divisible por 3 para cualesquiera m y n enteros. Para
ver que ello es así, aplicamos lo visto en párrafos
anteriores. Tenemos
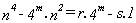
y la divisibilidad dependerá de que (r-s) sea múltiplo
de 3. resulta :
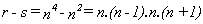
Y, evidentemente, para cualquier valor de n, alguno de
los números (n-1), n, (n+1) es múltiplo
de 3.
EJEMPLO 9.-
La expresión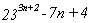 
[4]
no es múltiplo de 7. Para verlo, tenemos que 7n
siempre es múltiplo de 7, por lo que si la expresión
dada no lo es, debemos aplicar lo dicho a :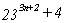
y tenemos :
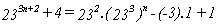
La expresión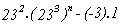 
siempre
es múltiplo de 7 puesto que tenemos :
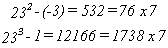
En consecuencia, por no ser 1 multiplo de 7, no lo será
la expresión inicial.
EJEMPLO 10.-
La expresión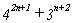 
[4]
es múltiplo de 13 para cualquier n entero. Tenemos
:
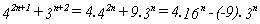
y como se verifica que : 16 - 3 = 13 ; 4 - (-9) = 13,
queda demostrado lo dicho.
BIBLIOGRAFIA
1.- M. Queysanne. Algebra básica, Ed. Vicens-Vives.
2.- A. Vera Lopez y R. Esteban Romero. Problemas y ejercicios
de matemática discreta, Ed A.V.L.
3.- T.M. Apostol. Introducción a la teoría
analítica de números. Ed. Reverté
4.- E. Bujalance, J. A. Bujalance, A.F. Costa, E. Martínez.
Elementos de Matemática discreta, Edit Sanz y Torres.
TEORÍA
DE NÚMEROS 