ALGUNAS APLICACIONES DE LOS RESIDUOS CUADRATICOS.

Recordamos que un número a es residuo cuadrático [1] de un primo q, si existe un valor n para el que se cumple (1):



Según el criterio de Euler, tenemos (2) :



Cuando el resultado es +1, decimos que a es residuo cuadrático módulo p, y cuando el resultado es -1, decimos que a es No residuo cuadrático módulo p.

TEOREMA

Para todo primo p = 4n+1, si m es un residuo cuadrático módulo p, entonces -m también es un residuo cuadrático módulo p. Para todo primo p = 4n+3, si m es un residuo cuadrático módulo p, entonces -m no es un residuo cuadrático módulo p.

Demostración

Considerando el símbolo de Legrende se cumple (3):



Según el pequeño teorema de Fermat y el criterio de Euler, siendo p un primo impar, tenemos para todo m (4) :



Por lo que si p = 4n+1 (5):



y si p = 4n+3 (6):



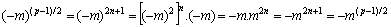
y queda demostrado lo que nos proponíamos.

Las propiedades de los residuos cuadráticos nos permiten caracterizar algunos primos para los cuales es posible deducir a priori algún factor de .

Sean p y q = 2p+1 primos ; existirán valores a y b que serán simultánea o alternativamente residuos cuadráticos respecto al primo q; es decir , se tendrá alguna de las posibilidades (a SR, b SR), (a SR, b NR), (a NR, b SR), (a NR, b NR) que, para el tema que nos ocupa, pueden reducirse a las dos primeras (7) :



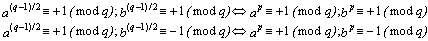
De las que es fácil deducir criterios de divisibilidad .

Para 2 tenemos (8):



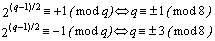
Con lo que los primos p tales que q =2p+1 es un factor primo de 2^p+1 ó 2^p-1, son (9) :



Para 3 tenemos (10) :



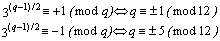
Con lo que los primos p tales que q =2p+1 es un factor primo de 3^p-1 , son (11) :



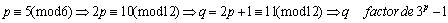
No existe ningún primo q para el que 3 sea un no residuo cuadrático y tal que (q-1)/2 sea primo.
Para 4 tenemos : 4 = 2², con lo que dicho valor es residuo cuadrático para todo primo > 3 y, por lo tanto, todos los números p = (q-1)/2 que sean primos darán un valor múltiplo de q para (4^p-1)/3.
Para 5 tenemos (12) :



Con lo que los primos p tales que q =2p+1 es un factor primo de 5^p+1 ó 5^p-1, son (13) :



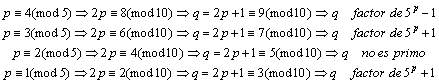
Para 6 tenemos que este número será residuo cuadrático cuando lo sean o no lo sean, simultáneamente, 2 y 3. Y tenemos :



Tenemos cuatro casos distintos en los que 2 y 3 son simultáneamente residuos cuadráticos (15):



Repitiendo el proceso cuando 2 y 3 son simultáneamente No residuos cuadráticos, llegamos al resultado (16):



Con lo que los primos p tales que q = 2p+1 es un factor primo de 6^p+1 ó 6^p-1, son (17) :



Para 7 tenemos (18) :



Con lo que los primos p tales que q = 2p+1 es un factor primo de 7^p+1 ó 7^p-1, son (19):



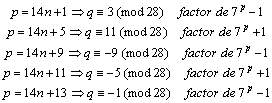
Para 8 tenemos la misma situación que para 2, es decir, los primos p tales que q = 2p+1 es un factor primo de 8^p+1 ó 8^p-1, son los que cumplen (9).
Para 9 tenemos : 9 = 3², con lo que dicho valor es residuo cuadrático para todo primo > 7 y, por lo tanto, todos los números p = (q-1)/2 que sean primos darán un valor múltiplo de q para (9^p-1)/3.
Para 10 tenemos una situación análoga a 6, y operando de modos similar resulta (20) :



Con lo que los primos p tales que q = 2p+1 es un factor primo de 10^p+1 ó 10^p-1, son (21) :



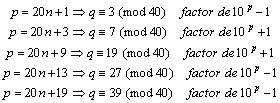
Para otros números tendríamos desarrollos análogos.

EJEMPLOS

Si p y q = 4p+1 son números primos, entonces 2 y 3 son raices primitivas de q y se cumple (22):



Demostración

Según el pequeño teorema de Fermat, podemos escribir (23) :



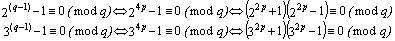
Sólo uno de los factores de cada una de las expresiones anteriores es múltiplo de q, pues en otro caso, restando un factor de otro, resultaría que 2 divide a q lo cual es imposible por ser q un número primo impar.

Por otro lado, todo primo impar puede escribirse en la forma p = 2n - 1 y todo primo impar, salvo el 3, puede escribirse en una de las formas (p = 3n+1 ó p = 3n+2). Según eso (24) :



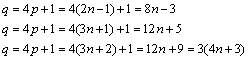
De la primera ecuación de (24) se deduce que 2 es un NO residuo cuadrático módulo q y, por lo tanto, se cumplirá (25) :



De la segunda ecuación de (24) se deduce que 3 es un NO residuo cuadrático módulo q y se cumplirá (26) :



Es trivial verificar que (27) :



para cualquier primo q tal que q = 4p+1, por lo que ambos valores cumplen las condiciones para ser raices primitivas módulo q.

Finalmente, de (25) y (26) resulta (28) :



y hemos demostrado lo que nos proponíamos.

Si p y q = 6p+1 son números primos, se cumple (29) :



Demostración

Según el pequeño teorema de Fermat, podemos escribir (30) :



Sólo uno de los factores de cada una de las expresiones anteriores es múltiplo de q, pues en otro caso, restando un factor de otro, resultaría que 2 divide a q lo cual es imposible por ser q un número primo impar.

Por otro lado, todo primo impar puede escribirse en la forma p = 2n + 1 y todo primo impar puede escribirse en una de las formas (p = 4n+1 ó p = 4n+3). Según eso (31) :



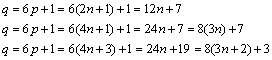
De la primera ecuación de (31) se deduce que 3 es un NO residuo cuadrático módulo q y, por lo tanto, se cumplirá (32) :



De la segunda ecuación de (31) se deduce que 2 es un residuo cuadrático módulo q y se cumplirá (33) :



De la tercera ecuación de (31) se deduce que 2 es un NO residuo cuadrático módulo q y se cumplirá (34) :



BIBLIOGRAFIA

1.- Apóstol, T.M. Introducción a la teoría analítica de números. Ed. Reverté
2.- A. Vera Lopez y R. Esteban Romero. Problemas y ejercicios de matemática discreta, Ed A.V.L.
3.- Aparicio, E., Teoría de los Números, Servicio Editorial U.P.V.
4.- Cilleruelo, J. ; Córdoba, A., La teoría de los Números, Biblioteca Mondadori.

EJERCICIOS Y PROBLEMAS RESUELTOS

MANUALES Y MONOGRAFIAS MATEMÁTICAS